СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ПРИ КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ

Рассмотренные выше приемы и методы статистического оценивания предполагали, что имеется выборка (xi, Xz, …. Хі, …, хп) результатов независимых испытаний при беско­нечной (или практически бесконечной) генеральной совокупности, В ЭТИХ условиях «извлечение» ИЗ совокупности наблюдения Xi не изме­няет распределения генеральной совокупности.

На практике часто приходится оценивать параметры генеральной совокупности, состоящей из конечного числа объектов N. Тогда можно считать, что оцениваемое свойство генеральной совокупности описыва­ется значениями функции X в N точках: хь х2, …. xj, …, xN. Будем полагать, что функция вероятности случайной величины X имеет вид

вер(Х = xj) = P(xj) = UN. (5.106)

Если г элементов в совокупности имеют одинаковое значение х, то

р(х’) — r/N. (5.107)

В частности, если в генеральной совокупности элементы имеют только два значения X (например, xt = 1 — работоспособный элемент, х2 = 0 — неработоспособный), то

р(л:,) = (N — M)!N р(х2) = MIN, (5.108)

где М — число неработоспособных элементов среда N элементов гене­ральной совокупности.

Пусть Xj, жа, …, Х[…… хп — безвозвратная выборка из генеральной

совокупности. При этом наблюдения х; в выборке зависимы, так как после каждого извлечения из генеральной совокупности одного эле­мента меняется вероятность последующих наблюдений значений xj.

Функция вероятности выборки

Математическое ожидание и дисперсия генеральной совокупности будут

N тЪ’* /=!	(5.110)
N
, ^ (xi тх?.	(5.111)

/=і

Доказано (см. [681), что и в этом случае несмещенной оценкой математического ожидания (5.110) является выборочное среднее

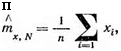(5.112)

а для дисперсии генеральной совокупности — выборочная дисперсия

(5.113)

Дисперсия оценки математического ожидания (5.112) (см. Г68І)

D А, N ] = < „ = (1 /Я — 1Ш) < д.»(1/п — 1/ЛО o2Xt N, (5.114) откуда

— К1/”— о<іЛГ» Ki/n— Ш aJCjw. (5.115)

Из (5.114) видно, что при объеме выборки, совпадающем с объемом генеральной совокупности, дисперсия оценки математического ожида­ния равна нулю. Это условие очевидно, оно отражает тот факт, что характеристика генеральной совокупности при п = N становится достоверной [см. (5.110)1.

Оценка математического ожидания является линейной функцией величин xt, которые имеют такое же распределение, как и xjt т. е. как

Л

генеральная совокупность. Если принять распределение оценки mXjN [см. (5.110)1 близким к нормальному с ат<к [см. (5.115)1, то можно легко рассчитать двусторонний и односторонний доверительные интервалы

Л

оценки тх, используя зависимости, аналогичные (5.28) и (5.29):

Л Л

mX, N-~Ul+]°m, N<moc^mx, N +ИЬИ °m, N’ (5Л16>

2 2

А

тх — и at (5.117)

Однако надо помнить, что в этом случае мы используем положение об асимптотической сходимости выборочного среднего к нормальному распределению при независимости наблюдений и в то же время рассчи­тываем дисперсию c? myN при конечной генеральной совокупности, дающей зависимую и малую выборку.

Пример 5.23. В условиях примера 5.1 найти доверительный интервал, если генеральная совокупность содержит N — 10 и 100 элементов.

По (5.115) найдем средние квадратические отклонения:

10 = J/1/9— 1/10 .1*0,105; од._ 100 = |Л/9 — 1/100 • 1 ~ 0,318.

Искомые доверительные интервалы:

3,12— 1,645 • 0,105 < тх < 3,12 -1- 1,645 — 0,105, или 2,95 < тх < 3,29;

3,12— 1,645 • 0,318 < тх < 3,12 + 1,645 • 0,318, или 2,60 С тх < 3,64.

В этих же условиях для бесконечной генеральной совокупности 2,57 с тх < 3,67.

Для случая, когда функция X генеральної! совокупности может принимать только два значения: Х = 1; лг2 = 0, математическое ожи­дание (5.110) принимает вид

mxN = р = (N — M)IN, (5.118)

где М — число элементов в генеральной совокупности С ЛГ2 = 0.

Величину Р можно определить как вероятность в первом испыта­нии извлечь из генеральной Совокупности элемент с xj = 1.

л

Несмещенной оценкой Р параметра Р в соответствии с (5.112) и (5.118) будет выражение, совпадающее с оценкой максимального прав­доподобия для параметра биномиального распределения (5.12):

mxN^=P=n — т) / п = 1—т/п. (5.119)

В соответствии с (5.113) и (5.119) оценка дисперсии распределения

m)(l — Pf + mP2] = _p)2 +

+ n (l — p) P2] = [p (l — p) + P2] = t

n — 1 n — 1

T. e.

k. N- Vnp(-p)J{n-). (5.120)

В соответствии с (5.115) и (5.120) среднее квадратическое откло-

л

нение оценки Р (5.119) принимает вид

Ш)п |/p(l_p)/(n-l). (5.121)

Нетрудно заметить, что при п = N получим ct,„iJV = 0, т. е. значе­ние математического ожидания распределения будет оценено досто­верно. Наконец, при Л/-э-оо выражение (5.121) упрощается:

V „ = Op = ]/p(l-p)/(n-l), (5.122)

т. е. совпадает со средним квадратическим отклонением оценки пара­

метра биномиального распределения (5.13).

Таким образом, при малой генеральной совокупности можно коэф­фициентом

KN = Vn(l/n — 1 IN) = V(N — n)/N (0 < КN< 1) (5.123)

учитывать уменьшение дисперсии оценки среднего значения за счет того, что выборка соразмерна с объемом генеральной совокупности. Заметим, что в работе [311 предлагается использовать близкий к (5.123) коэффициент [/(IV — n)/(N — 1).

При безвозвратных выборках объема п из конечной генеральной совокупности объема N, элементы которой могут обладать каким-либо

Л* пп—X

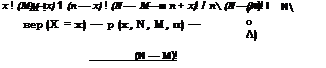признаком или не обладать (величина Xj имеет два значения), случай­ная величина числа элементов х в выборке, обладающих данным приз­наком, имеет гипергеометрическое распределение (см. табл. П.1):

где М ности.

Математическое ожидание и дисперсия гипергеометрического рас­пределения определяются выражениями

Мх = тх = пМ/N; D [х] = о* = -^Lf 1— — ) (1 — —М. * N N ) N— 1 )

(5.125) [(5.126)

л л

Для определения величины М1в по параметрам п, т, N и у имеются таблицы (см. [7]), составленные для я < 25 и N — Ж 25. В них

Л Л Л

приведены значения п — (Мів — т) как функции от п, N — пит

Л Л

при ух = 0,95. Величину Мів — т можно рассматривать как односто­ронний верхний доверительный предел числа элементов с данным приз­наком, оставшихся после выборки в генеральной совокупности. Таким образом, в соответствии с (5.118) для генеральной совокупности истин­ное значение доли изделий, обладающих данным признаком (например, неработоспособным состоянием),

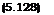
Р = 1 — MIN.

Несмещенная оценка этой величины

Л Л,

Р — 1 — min,

л

среднее квадратическое отклонение оценки Р будет

односторонний нижний доверительный предел

Pi»,N = 1 —MJN, (5.131)

Л

где Мі к определяется по таблицам [7].

Величина

Р1Н w_n) — 1 — (/И1в — т) /(N — n) (5.132)

является нижним односторонним доверительным пределом доли изде­лий, обладающих данным признаком из оставшихся после выборки в генеральной совокупности.

Верхним пределом доли изделий в генеральной совокупности, обладающим данным признаком, будет не единица, а

(5.133)

так как после выборки достоверно известно, что по меньшей мере т изделий обладали данным признаком. Следовательно, справедливы неравенства

вер {l — MUl/N < M/N < 1 — гп/n} > у,, (5.134)

вер {l —(М1в— m)l(N — п) С (М — m)l(N —п) с l} > уг (5.135) Для малой выборки, когда выполняется условие

п<0,Ш, (5.136)

гипергеометрическое распределение (5.124) сходится к биномиальному с параметрами п и M/N =1 — Р:

р (а, п, N, М) ж р (л-, п, Р) = —— ——— (1 — Р)х, (5.137)

х I (п — х)!

где х в общем случае может быть и дробным числом.

В этом случае для определения доверительных интервалов оценки

Л

Р (5.129) могут быть использованы табл. П.10 и П.11, а также пуассо­новская аппроксимация (5.41)—(5.43) или нормальное приближение (5.45)-~(5.46). При использовании нормального приближения в соот­ветствии с (5.29), (5.45), (5.46) и (5.121) — (5.123) односторонний ниж-

л /■

ПИЙ доверительный предел Р 1Н, д- оценки Р определяется выражением

Л	/Л	) (Г’
Р 1н, N — ^п, 1	(Р~	— % °т, J = Кп. тр — аР>

(5.138)

Если величины п, N — п, М, N — М не слишком малы, что обычно определяется условием

то гипергеометрическое распределение можно аппроксимировать нор­мальным

1 — (х—m )2//2з2

р (х, N, п, М) ж——— —е х ‘ (5.140)

V 2*

где /пЛ., о2т определяются по (5.125) и (5.126).

Пример 5.24. Из генеральной совокупности, содержащей N = 100 изделий, •сделана безвозвратная выборка п = 10 изделий, среди которых одно было не-

Л

работоспособным (т = 1). Найти односторонний нижний доверительный предел

л

оценки Р доли работоспособных изделий при Yj = 0,95. Вычислим оценку (5.129): Р = 1 — 1/10 = 0,900 и ее среднее квадратическое отклонение [см. (5.130)]: ар< N = V 10(1/10—1/100) У 0,900(1 —0,900)/(10— 1) =

= 0,949 • 0,100 = 0,0949.

По табл. ГІ.7 находим квантиль а0 ^(1) = 4,744 распределения Пуассона.

Л

По зависимости (5.43) имеем Р1Н(дг = (2 • 10— 1 — 4,744)/(2 • 10 — 1 + + 4,744) = 0,600. Используя менее точное нормальное приближение (5.138) и <5.47), получим

л

Р1н д, =(1 — 1,80/10) (0,900— 1,645 • 0,0949) = 0,610.