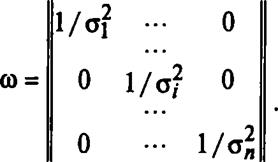Методы определения оценок нестационарных параметров

Приведенные материалы по определению результатов испытаний предполагают их постоянвгво при проведении выборочного экспери­мента. Однако процессы, протекающие при функционировании тех­нических систем, часто являются существенно нестационарными.

Статистический анализ нестационарных процессов чрезвычайно сложен. Поэтому для получения инженерных результатов нестацио­нарный процесс представляется в виде композиции неизвестных по­стоянных параметров и известных функций времени. При этом наи­более распространена полиномиальная аппроксимация:

^(0= Х0у/у(О> (10.4)

у=1

где 0. — неизвестные постоянные коэффициенты; fj (/) — известные функции времени.

В качестве функций fj (t) часто выбирают различные степени

аргумента t. В этом случае зависимость (10.4) в дискретной форме для /-го интервала времени имеет вид:

б(/Д/) = 00+01 (iAt) +… + 0* (iAtf, где i=l, 2, …

Для удобства дальнейших выкладок запишем зависимость (10.4) в матричной форме:

d = XQ,

где dT = |dj,…,6J-,…,flJ — вектор значений оцениваемого нестацио­нарного параметра;

1 At… (Дtf

1 iAt… (iAty

і • •

1 nAt… (лД/У

0Т = |0g,…,0y,…,0j| — вектор неизвестных параметров; п — чис­ло дискретных моментов времени; к+1 — число неизвестных парамет­ров, т — индекс транспонирования.

Модель измерений в рассматриваемом случае носит название си­стемы условных уравнений:

ZT = ЛГ0 + 8Т,

где ZT = fa,—,Zi, II — вектор измерений нестационарного пара­метра; 8Т = ||8і,…,8|-,…,8и| — вектор ошибок измерений.

Неизвестные параметры 0 находят методом наименьших квадра­тов (м. н.к.) из условия минимизации функционала:

S2 = (Z — Z0)T co(z — *0),

где а> — матрица весовых коэффициентов.

Если априорная информация о статистических характеристиках

ошибок измерений отсутствует, то © = 1„ (единичная матрица).

При многомерном нормальном законе ошибок измерений

8~Лг(0, а2с),

где 0 — нуль-векгор математических ожиданий; а2С — ковариаци­онная матрица ошибок измерений, выбирается © = (а2Сj — весо — вая матрица.

Если ошибки измерений статистически независимы, то ю явля­ется диагональной матрицей

При равноточных измерениях а2 = …= а2 =…= имеем со = 1 /а2.

Оценки наименьших квадратов находятся решением системы нор­мальных уравнений или

XTtoXQ = X^ti>Z,

откуда 0 = (irB(oir) f^Bcaz).

Точность оценок наименьших квадратов характеризуется диспер­сионной матрицей D(ej = fjfBcozj.

Оценкой наименьших квадратов искомого показателя •& в ;-й мо­мент времени является оценка д,- = Aj0, D(6,) = ^D(0)JTB, где Х( — /-я строка матрицы X.

В табл. 10.9 приведены примеры использования полиномиаль­ной аппроксимации. При аппроксимации полиномом возникает воп­рос о выборе степени этого полинома. Обычно аппроксимацию на­чинают с использования простейших полиномов (нулевого или первого порядка), а затем, по мере необходимости, порядок повышают.