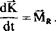МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОСТРАНСТВЕННОГО ДВИЖЕНИЯ САМОЛЕТА

2.1. УРАВНЕНИЯ ДВИЖЕНИЯ

Пространственное движение самолета описывается системой дифферен­циальных уравнений. В главе 1 были введены понятия собственного и вынужденного, поступательного и вращательного движений самолета. Вывод уравнений удобно провести отдельно для каждого из перечисленных видов движения с последующим их объединением в общую математи­ческую модель пространственного движения самолета.

Уравнения собственного поступательного движения. Собственное посту­пательное движение самолета описывается системой динамических и кине­матических дифференциальных уравнений. Динамические уравнения описы­вают движение центра масс самолета относительно Земли и позволяют установить зависимость между параметрами поступательного движения самолета относительно Земли (земной скоростью v„, углом пути *Р, углом наклона траектории 9) и параметрами движения самолета относительно воздушного потока (углом атаки а, углом скольжения р, скоростным углом крена уа). ■

Динамические уравнения получаются из векторного уравнения для количества движения относительно центра масс самолета:

dv _

m-^FK, (2.1)

где m-масса самолета; Р,- вектор сил, действующих на самолет в траекторией системе координат.

От векторного уравнения (2.1) перейдем к скалярным уравнениям. Для этого определим проекции вектора dvK/dtHa соответствующие оси. Так как траєкторная система координат вращается относительно нормальной с угловой скоростью ш*к, проекции производной вектора vK можно опре­делить следующим образом:

(^)v = V, I cdZi Vx> — к>х, vz_; (2.2)

(^)/Vz>+Cq[> Vy2K-av VX(,

где Vv Vy>1 V* — проекции вектора скорости vK на оси траекторией системы координат; , V^- проекции производной вектора скорости на оси траекторией

системы координат; юх, <ву, coz — проекции вектора угловой скорости со а вращения траекторной системы координат относительно Земли на траекторные оси.

2 Зач. 948 33

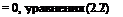
С учетом того что Vx = VK; Vy = V2 = 0; Vy упрощаются:

Определим кинематическую связь проекций вектора СО* угловой ско­рости вращения траекторной системы координат относительно нормаль­ной с углами и их производными, характеризующими положение траектор­ной системы координат относительно нормальной:

шх = * sm 6; шу = *cos0; юг = 6. (2.4)

Примем допущение об отсутствии ветра, тогда значение земной скорости V„ совпадает со значением воздушной скорости V, = V и вектор­ное уравнение (2.1) с учетом уравнений (2.2)-(2.4) примет следующий скалярный вид:

mV = FXi; mV0 = Fy>; — mV* cos 9 = FZj, (2.5)

где Fx, Fy, Fz — проекции вектора сил Р, на оси траекторной системы координат.

Рассмотрим правую часть системы уравнений (2.5). Движение центра масс самолета в основном определяется действием трех видов сил: вектора тяги двигателей Р, вектора аэродинамической силы RA и вектора силы тяжести самолета <3. Спроецировав эти силы на оси траекторной системы координат, получим:

Fx_ = Рх< + RA, + G, ; F„ = Pv + Rai + Gv ;

рч’+ Kn*+GXi ‘ ”

При этом мы пренебрегаем действием кориолисовой силы инерции и переносной силы инерции, связанных с вращением Земли. Для получения проекций вектора тяги Р воспользуемся матрицей направляющих косину­сов (см. табл. 1 приложения), позволяющей перейти от связанной системы координат к траекторной: ■

Рх = Р cos a cos р; Ру = Р (sin а cos ya + cos a sin р sin yj; ^

Pz = P(sin авіпуз —cos авіп рсовуД.

В уравнениях (2.7) предполагается, что тяга двигателей Р, лежащая в плоскости симметрии самолета ХОУ, составляет с осью ОХ угол (рР = 0. В пртивном случае этот угол необходимо прибавить к углу атаки а.

Для получения проекций вектора аэродинамической силы RA на траекторные оси координат воспользуемся допущением об отсутствии ветра. Тогда траєкторная система повернута относительно скоростной на угол уа вокруг оси ОХа. Поэтому проекции аэродинамической силы RA на оси траекторной системы координат выражаются через проекции на скоростные оси:

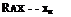RAy, = Y. cosy, — Zasmya;

Сила тяжести самолета С приложена в его центре масс и направлена вниз по местной вертикали. Следовательно, она расположена в плоскости OXKYK траекторной системы координат и ее проекции имеют вид:

Gx=—mgsinG; Gy = —mgcosG; GZj = 0. (2.9)

Подставим выражения (2.6)-(2.9) в правую часть системы уравнений (2.5). Тогда с учетом зависимости сил от параметров движения (1.8), (1.11)—(1.13) получим следующую систему динамических уравнений собст­венного поступательного движения центра масс самолета в проекциях на оси траекторной системы координат:

mV = Р(М, ря, Тн, р, V) cos ct cos Р — Ха(а, М, р, V) — mg sin G =

= FX>, р, 0, М, V, р, рн, Тн);

mVG = Р(М, рн, Тн, р, V) [sinacosya + cos а sin Р sin ya] + + Ya(a, М, р, V)cosya — Za(P, р, V)sinya — mg cos в =

= Fy>, P, 0, ya, M, V, p, pH, TH);

— mV’!’ cos 0 = Р(М, рн, Тя, р, V) [sin a sin ya — cos a sin p cos ya] +

+ Ya (а, M, p, V) sinya + Za(p, p, V)cosya =

= Fz>(a, p, ya, M, V, p, pH, TH).

Продолжим построение математической модели собственного поступа­тельного движения самолета, дополнив систему динамических уравнений (2.10) кинематическими уравнениями. Эти уравнения позволяют установить зависимость между параметрами положения самолета в поступательном движении относительно Земли (пройденным расстоянием L, боковым отклонением 2, высотой полета Н) и параметрами этого движения (воздуш­ной скоростью V, углом пути Ч* и углом наклона траектории 6).

Кинематические уравнения поступательного движения описывают дви­жение центра масс самолета относительно Земли. Вектор земной скорости самолета vK определяется проекциями на нормальные оси с помощью таблиц направляющих косинусов (см. табл. 1 приложения). Учтем тот факт, что оси нормальной системы координат параллельны осям нормальной земной системы координат. При допущении отсутствия ветра Vr = V координаты самолета в нормальной системе координат xg, yg, zg удобно заменить на параметры положения самолета L, Н, 2. Тогда

Система динамических уравнений (2.10) и система кинематических уравнений (2.11) представляют собой математическую модель собствен­ного поступательного движения самолета.

Уравнения собственного вращательного движения. Собственное враща­тельное движение самолета описывается системой динамических и кине — 2* 35

матических дифференциальных и алгебраических уравнений. Динамические уравнения описывают движение самолета относительно его центра масс и позволяют установить взаимосвязь параметров вращательного движения самолета (скоростей крена сох, рыскания юу и тангажа со2).

Динамические уравнения получают из векторного уравнения для глав­ного кинетического момента относительно центра масс количества движе­ния-самолета как твердого тела К.:

(2.12)

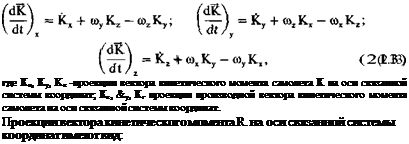
От векторного уравнения (2.12) перейдем к скалярным уравнениям. Для этого определим проекции вектора dK/dt на оси связанной системы координат. Так как проекции производной вектора К зависят от составляю­щих угловой скорости со вращения связанной системы координат относи­тельно Земли, то система скалярных уравнений определяется следующим образом:

(2-14)

где Jx, Jy, їх — осевые моменты инерции самолета; J, JI2, Jyz — центробежные моменты инерции самолета. ‘

Моменты инерции самолетов с меняющейся в полете массой вследствие выгорания топлива являются в общем случае функциями времени, однако мы этой зависимостью пока будем пренебрегать.

Поскольку основная плоскость OXY связанной системы координат является плоскостью симметрии самолета, то центробежные моменты инерции, содержащие координаты 2, равны нулю: Jxz = Зуг = 0. Тогда система уравнений (2.13) упрощается:

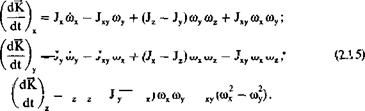
Jx®x — JxA + (J* — Jy)®y®2 + J JA A“x +(Jx-Jz)®x®

JA + (Jy-Jx)coxG)y — Jxy(o>; — Юу) = MR^(a, а, Р, юг, М, р, V, рн, Тв).

Продолжим построение математической модели собственного враща­тельного движения самолета, дополнив систему динамических уравнений (2.16) кинематическими уравнениями. Эти уравнения описывают враща­тельное движение самолета относительно Земли и позволяют установить зависимость между параметрами положения самолета во вращательном движении относительно Земли (углами крена у, рыскания у, тангажа о) и параметрами этого движения (скоростями крена сох, рыскания соу и тангажа таг).

Вектор угловой скорости самолета со относительно нормальных осей равен геометрической сумме угловых скоростей связанной системы коор­динат. Поэтому векторное кинематическое уравнение вращательного движения самолета записывается следующим образом:

ю =Tj + у + о. (2.17)

Проецируя векторы у, и С на оси связанной системы координат, получим скалярную систему уравнений:

Решим систему уравнений (2.18) относительно у, |/ и 0, получим необходимые кинематические уравнения:

у = сйх — tg и (о cos у — coz sin у); у = sec и (юу cos у — юг sin у); (2.19)

0 = <Оу sin у + 0)2 С08 у.

Система динамических уравнений (2.16) и система кинематических уравнений (2.19) представляют собой математическую модель собствен­ного вращательного движения самолета. Таким образом получены 12 уравнений движения самолета, связывающих между собой 15 параметров положения и движения самолета. Для того чтобы система уравнений стала замкнутой и имела решение, необходимы еще три уравнения. Эти уравне­ния получим, установив геометрические соотношения между углами, определяющими параметры положения и движения самолета.

Пользуясь таблицей направляющих косинусов (см. табл. 1 приложения), можно путем определенных преобразований получить взаимосвязь между параметрами положения и движения самолета в связанной системе

37

координат (у, у, и), скоростной системе координат (а, Р, уа) и траекторией системе координат (¥, 0). При отсутствии ветра эта связь определяется следующим образом:

sin а = {[sinи cosy созО? — у) + sinувіпОР — v)] cos 9 —

— sin 0 cos и cos у}/cos р;

sin р = cos 0 [^usm у cos OF — у) — cos у sin OF — у)] — (2.20)

— sin 0cosusiny;

sinya = [cosа sin р sin и — соз n (sinа sin Р cos у — cos р siny)]/cos 0 .

Таким образом, математическая модель собственного движения само­лета содержит систему динамических (2.10) и систему кинематических (2.1 1) уравнений поступательного движения, систему динамических (2.16) и систему кинематических (2.19) уравнений вращательного движения, а также систему уравнений геометрических соотношений (2.20).

Уравнения вынужденного движения. Дополним полученную математи­ческую модель собственного движения вынужденной составляющей под действием внешних возмущений и управлений. Ветер изменяет проекции вектора тяги Р и вектора аэродинамической силы на оси траекторной системы координат. С учетом зависимостей сил, действующих на самолет от управляющих воздействий и внешних возмущений (1.45), система динамических уравнений поступательного движения самолета (2.10) пре­образуется следующим образом:

mV = Р(М, рн, Тн, р, V, 5Р) соз(а — aw) cos(p — Pw) — — Ха(а, М, р, V, 5Х, fx)cosaw созРуу +

+ Ya(a, М, р, V, 5у, fy)sinawsinpw —mg sin 0 =

= Fx (a, р, 0, М, V, р, рв, Тн, 5р, 5Х, 5у, fx, fy, aw, pw);

mV0 = Р(М, рн, Тн, р, V, 8P) [sin (a — aw) cosya +

+ cos (а — aw) sin (P — Pw) sin ya] +

+ Xa(a, М, р, V, 8X, fx) sinaw зтР№ +

+ Ya (а, М, р, V, 8у, fy) cosya cosaw созРуу — (2.21)

— Za(P, р, V, 5Z, fz) sinya — mg cos0 =

= Fy_(a, p, 0, M, V, p, pH, TH, 8p, 8X, 8y, 5Z) fx, fy, fz, aw, pw);

— mV^cosO = Р(М, рн, Тн, р, V, 5P) [sin(a — aw) sinya —
— cos (а — aw)sin(P —Pw)cosyJ +

+ Ya (a, M, p, V, 8y, fy) зтуа + Za (p, p, V, 5Z, fz) созуа =

= Fz (a, P, уа, M, V, p, pH, TH, 8P, 8y, 8Z, iy, f2, aw, pw).

С учетом зависимостей моментов, действующих на самолет, от управляющих воздействий и внешних возмущений (1.46) система динами­ческих уравнений вращательного движения самолета (2.16) имеет вид:

— ^ху^у + (^2 Jy) ®у^ЗЕ + ^ху^х^у ^ Мх(Р, G6 й)х» ^у» ‘

. р, V, §„ sH>mxB);

Jyffly — Jxyfflx + (Jx — JJ<ax<»z — Jxy®y<az = My(P, а, шх, юу,

p, V,63)SH, myJ; (2.22)

JA + (Jy — ^ox(oy — Jxy(to;; — Юу) =

= MR,(a, а, Р, юг, М, р, V, рн, Т„, 8Р, 5В, cp, mZB).

Система кинематических уравнений поступательного движения (2.11) и система кинематических уравнений вращательного движения (2.19) остаются без изменений. В геометрических соотношениях (2.20) следует учесть составляющие ветра:

sin (a — aw) ~ {[sin и cos у cos (SP — ц/) + sin у sin (Ч/ — у)] cos 0 +

+ sin 0 cos и cosy}/cos(P Pw)>

Sin (Р — Pw) = COS 0 [sin 0 Sin у COS(*P — у) — СО5 у sin OF — y/)J —

— sin 9 cos и sin у; (2.23)

8т у = {cos(a — aw)sin(P — р*)8тіі — cos и [sin (a — aw)sin(P — p^cosy —
— cos(P — pw)siny]}/cos0.

Таким образом, математическая модель вынужденного движения самолета содержит систему динамических (2.21) и систему кинематических (2. И) уравнений поступательного движения, систему динамических (2.22) и систему кинематических (2.19) уравнений вращательного движения, а также систему уравнений геометрических соотношений (2.23).