УРАВНЕНИЯ ПРОДОЛЬНОГО ДВИЖЕНИЯ САМОЛЕТА. (В СПОКОЙНОЙ АТМОСФЕРЕ)

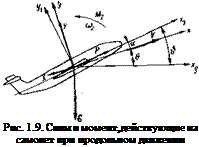
В продольной плоскости на самолет действуют сила тяжести G = mg (рис. 1.9), направленная по вертикали, подъемная сила У, направленная перпендикулярно скорости набегающего потока, сила лобового сопротивления X, направленная по скорости этого потока, и тяга двигателей Р, направленная к потоку под углом, близким к углу атаки а (полагая угол установки двигателей относительно оси Ох і равным нулю).

Продольное движение самолета наиболее удобно рассматривать в скоростной системе координат. В этом случае проекция вектора скорости на ось Оу равна нулю. Угловая скорость вращения каса­тельной к траектории движения центра масс относительно оси Ог

<ог= —В = & — а.

Тогда уравнения движения центра масс самолета в проекциях на оси Ох и Оу имеют следующий вид:

проекции сил на ось Ох (касательную к траектории):

mV = — X—Osm0-f-/°cosa; (1.2)

проекции сил на ось Оу (нормаль к траектории):

mVb = Y — G cos 0 — f~ Z3 sin a. (1.3)

Уравнения, описывающие вращение самолета относительно центра масс, наиболее простыми получаются в связанной системе

координат, поскольку ее оси сов­падают с главными осями инер­ции. Так как при рассмотрении изолированного продольного дви­жения полагаем р=0 (при этом условии скоростная система ко­ординат совпадает с полусвязан — ной) и, следовательно, ось Ог ско­ростной системы координат сов­падает с осью Ozi связанной системы, то уравнение моментов относительно оси Oz имеет вид[1]:

где /2 — момент инерции самолета относительно оси Ог;

Мг — аэродинамический момент тангажа, продольный момент.

Для анализа характеристик продольного движения самолета относительно его центра масс необходимо добавить уравнение свя­зи углов атаки, тангажа и наклона траектории:

* = 0. (1.5)

При рассмотрении динамики продольного траєкторного движе­ния самолета — движения его центра масс относительно земли — необходимы еще два кинематических уравнения:

xg = L*=V COS0; (1.6)

yg — H = V sin б, (1.7)

где Н — высота полета;

L — пройденное расстояние вдоль оси Oxg земной системы координат, кото­рая предполагается совпадающей по направлению с осью Ох скоростной системы.

В соответствии с гипотезой стационарности аэродинамические силы и моменты являются нелинейными функциями следующих параметров:

Х=Х(*% I7, М, Ря);

Г = Г(*9 1/, м, Ря);

M2 = Mz(bв. <*» а, V, М, рн),

: (ая “ скорость звука на высоте полета);

ря — плотность воздуха на высоте полета; бв — угол отклонения руля высоты.

Эти силы и моменты могут быть записаны через аэродинамиче­ские коэффициенты:

X=crS!‘V2

Y = ctJS

Mz=mzSbk — ї

где Cx — Cx (a, M) —коэффициент лобового сопротивления;

Су —Су (a, М) —коэффициент подъемной силы;
mz—mz (бв, a, a, d, M) —коэффициент продольного момента M%

S — площадь крыла самолета;

Ьа —средняя аэродинамическая хорда САХ.

Тяга двигателей также является нелинейной функцией ряда па­раметров:

Р = Р(8д) М, рн, Тя),

где бл — перемещение органа, управляющего тягой двигателей; ри —давление на высоте полета;

Тя — абсолютная температура воздуха на высоте полета.

Будем рассматривать в качестве невозмущенного движения ус­тановившееся прямолинейное движение

(V 0 — = %—®z0~ О)1* Тогда для невозмущенного движения система уравнений примет вид: — Х0 — G Sin 0О — f Р0 cos а0 = 0; (1.9) К0 —0 cos 0o-)-Posinao = O;. (ЇЛО) £ N о 11 О (1.11) «0 — ^о — ®0 >’ (1.12) (1.13) ^о=1/08ІГі60- (1.14) Полагаем, что параметры возмущенного движения могут быть выражены через их установившиеся значения и малые приращения:

V = VQ + W;

а = а0-4-Да;

Є-VU; <U5>

е = 60 + Д6.

Проведя с учетом (1.15) линеаризацию уравнений возмущенно­го движения (1.2—1.7) и принимая во внимание уравнения невоз­мущенного движения (1.9—1.14), получим систему линейных диф­ференциальных уравнений с постоянными коэффициентами [12]:

mbV = — XvbV — Xм ДМ —Х“Да— А^р&Д yg— G cos 0ОД0 — f + COS а0ДМ — P0 sin а0Да — f P? cos а0рйдyg -f P T COS а„Тун^Уе +

cos «0Д8д; (1.16)

mV^b = YVW + КмДМ + К“Да — f Кіу Дyg + О sin 0ОД6 +

+ рМ sin аоДМ + PQ cos а0Да — f P? sin а0р^Дyg +

+ P T sin *ъТу„Ьув + P5 sin а0Д5д; (1.17)

Izb = M ® Д8В — f M’M — f МІДа — f AlfbA — f [2]

+ MvzAV + МгЛ, ДМ+ М^Дуг;	(1.18)
Длг^ — (V0 — f AV) c os 0O — V0 s і n 0O Д0;	(1.19)
kyg’-^iV o + Д’7) sin0o — f1/0 cos 0оДб;	(1.20)
Д0 = д8 — Да.

дХ, дХ < vrp дХ •— — у — ‘ Л 1 — —— 3V да доя

В этих уравнениях для упрощения письма введены символиче­ские обозначения частных производных:

При исследовании динамики захода на посадку и посадки са­молета уравнения (1.16—1.18) могут быть упрощены за счет пре­небрежения (по их малости) членами, содержащими производные по параметрам р, Т, производными аэродинамических сил и их мо­ментов по числу М. По аналогичным соображениям производную Ям можно заменить производной Pv, а приращение ДМ — прира­щением XV. Кроме того, в уравнении моментов необходимо учесть, что Mzv = 0 и Мрг =0, поскольку коэффициент момента mZo = 0. Тогда уравнения (1.16—1.18) примут вид:

mAV=-XvAV — Х’1Ая — О cos 0ОД0 + Pv cos а0ДК —

— Р„ s і П а0Д а — f — Р5 cos а0Д&л; (1.16а)

mV0A<i = YVAV + Г Да + О sin 0ОД0 + P^sin а0Д1/ +

+ Я0 cos а0Да-(-Р8 sin а0Д8д; (1.17a)

1$ = Щ Д8В + м Да + М Да + Д 8;

Xv=cXoSpV0;

va а С Р V0

Yv=c!/oSpV0; Ya = cauS ;

(1-21)

ЖЇ —mazSb,

Г к ж—’*-»** * с. — д_

?vl .

M=m%Sbt

МІ =тІ SbA

£ Значения коэффициентов Cti Су, Cx, Су, niz, fflz, fflz, tftz Оп­ределяют с помощью графиков, составляемых на основании резуль­татов продувки моделей самолетов в аэродинамических трубах и летных испытаний самолета. Характеристики Рь необходимы при рассмотрении случаев, ког­да в возмущенном движении происходит перемещение органа, управляющего тягой, например, при рассмотрении продольного движения самолета, одновременно управляемого автопилотом и автоматом тяги (автоматом скорости). Если же в процессе возму­щенного движения Д6д=0, то последний член в уравнениях (1.16 и 1.17) равен нулю. Анализируя устойчивость движения неуправляемого самолета {с зажатыми органами управления), нужно учитывать, что устой­чивость такого движения совершенно не зависит от координаты хе и практически не зависит, вследствие пренебрежения влиянием Рн и Тн, от координаты yg. Поэтому при анализе устойчивости дви­жения самолета без системы автоматического управления уравне­ния (1.19 и 1.20) можно исключить из рассмотрения.

2 (_ ,P^jjn* o У 0 1 I, b’ * ■ C I! V* Q

‘111. r{

(1.23)

<”>n

т2?,2

mz’j. n

tf?2

l^o

Л, . « . Юг-^ =M-A. v0 K0

Заметим, что члены, содержащие управляющие координаты 6Д и 6В, находятся в правой части уравнений. Характеристический полином для системы уравнений движения неуправляемого само­лета (с зажатыми органами управления) имеет следующий вид:

А (р) = Р4 -f яjP3 + йоР2 + а3р — f д4, (1.24)

где йі = йу + £а—+ — f г — ;

+ — f с. + ^ь+с; )(«vr —60);

Й3 = Г« (rtK ~ + + + ^4 )(a6^V ~av b*)>

ai — ca{atbv — avbH).

Согласно критерию Гурвица-Рауса движение, описываемое уравнением четвертого порядка, устойчиво тогда, когда коэффици­енты аь а2, а3 и а4 положительны и а3(аіа2—аз)—а4аі2>0.

Эти условия обычно удовлетворяются не только для режимов захода на посадку, но и для всех эксплуатационных режимов поле­та дозвуковых гражданских самолетов. Корни характеристического полинома (1.24) обычно комплексно-сопряженные, различные по величине, и им соответствуют два различных колебательных движе­ния. Одно из этих движений (короткопериодическое) имеет малый период с сильным затуханием. Другое движение (длиннопериоди­ческое, или фугоидное) является медленно затухающим движением с большим периодом.

Вследствие этого возмущенное продольное движение может рассматриваться как взаимное наложение этих двух движений. Учитывая, что периоды этих движений весьма различны и что ко­роткопериодическое колебание сравнительно быстро затухает (за 2—4 сек), оказывается возможным рассматривать короткоперио­дическое и длиннопериодическое движения изолированно друг от друга.

Возникновение короткопериодического движения связано с на­рушением равновесия моментов сил, действующих в продольной плоскости самолета. Это нарушение может быть, например, резуль­татом воздействия ветрового возмущения, приводящего к измене­нию угла атаки самолета, аэродинамических сил и моментов. Вследствие нарушения равновесия моментов самолет начинает поворачиваться относительно поперечной оси Oz. Если движение устойчиво, то он вернется к прежнему значению угла атаки. Если же нарушение равновесия моментов произошло вследствие откло­нения руля высоты, то самолет в результате короткопериодического движения выйдет на новый угол атаки, при котором равновесие мо­ментов, действующих относительно поперечной оси самолета, вос­станавливается.

За время короткопериодического движения скорость самолета не успевает значительно измениться.

Поэтому при исследовании такого движения можно полагать, что оно происходит при скорости невозмущенного движения, т. е. можно принять ДУ—0. Полагая исходный режим близким к гори­зонтальному полету (0«О), можно исключить из рассмотрения член, содержащий Ьд.

В этом случае система уравнений, описывающих короткоперио­дическое движение самолета, принимает следующий вид:

Дб — &аДа=0;

Д б + е j Д& — f ск Да — f саДа == с5Дйв; Дб = Д& — Да.

Характеристический полином для этой системы уравнении имеет вид:

Л(/>)к = д(/>2 + аі/> + а. Ф где а=ьЛск+с> Ї

а2 = bSh+Cf )

Короткопериодическое движение устойчиво, если коэффициенты «і и 02 положительны, что обычно и имеет место, поскольку в об ласти эксплуатационных режимов величины b*, сх, г» и сущест­венно положительны.

Характеристический полином (1.26) имеет следующие корни:

Отрицательная действительная часть корней /?і,2 указывает на то, что с течением времени отклонение угла атаки от исходного значе­

V*-4

ния стремится к нулю. При этом величина

частоту собственных колебаний самолета в короткопериодическом движении, а величина ——- их затухание. Первая величина определяется главным образом коэффициентом ml, характеризу­ющим степень продольной статической устойчивости самолета. В свою очередь коэффициент ml зависит от центровки самолета, т. е. от взаимного расположения точки приложения аэродинамиче­ской силы и центра масс самолета.

Вторая величина, обусловливающая затухание, определяется

в большой степени коэффициентами моментов mlz и т% ■ Коэффи­циент т’"гг зависит от площади горизонтального оперения и его расстояния от центра масс, а коэффициент ml еще и от запаздыва­ния скоса потока у оперения. Практически, вследствие большого затухания, изменение угла атаки имеет характер, близкий к апе­риодическому.

Нулевой корень р3 указывает на нейтральность самолета отно­сительно углов д и 0. Это является следствием сделанного выпи упрощения (ДУ = 0) и исключения из рассмотрения сил, связанным с изменением угла тангажа, что допустимо только для начального периода возмущенного продольного движения — короткопериоди ческого *. Изменения углов A# и ДО рассматриваются в длиннопе риодическом движении, которое упрощенно можно считать начина­ющимся после окончания короткопериодического движения. При

1 Подробно по этому вопросу см [26].

этом Ла=0, а величины углов тангажа и наклона траектории отлич­ны от значений, имевших место в исходном невозмущенном движе­нии. Вследствие этого нарушается равновесие проекций сил на касательную и нормаль к траектории, что приводит к возникнове­нию длиннопериодических колебаний, в процессе которых происхо­дят изменения не только углов О и 0, но и скорости полета. При условии устойчивости движения равновесие проекций сил восста­навливается и колебания затухают.

Таким образом, для упрощенного исследования длиннопериоди­ческого движения достаточно рассмотреть уравнения проекций сил на касательную и нормаль к траектории, полагая Да = 0. Тогда сис­тема уравнений продольного движения принимает вид:

(1.28)

Характеристический полином для этой системы уравнений имеет вид:

где ai = av—b^ a2=abbv — avbb.

Устойчивость движения обеспечивается при условии «і >0; й2>0. Затухание колебаний существенно зависит от значений про­изводной Pv и коэффициента сХа, а частота собственных колеба­ний— еще и от коэффициента су„ поскольку эти коэффициенты определяют величины проекций сил на касательную и нормаль к траектории.

Следует отметить, что для случаев горизонтального полета, на­бора высоты и снижения с малыми углами 0 коэффициент Ьв имеет очень малую величину. При исключении члена, содержащего

из второго уравнения (1.28) получаем at = av; a2 = aebv.