РАСЧЕТ СТАЦИОНАРНОГО КОНТУРА ТЕЛЕУПРАВЛЕНИЯ ПО КРИТЕРИЮ МИНИМУМА ДИСПЕРСИИ ЛИНЕЙНОГО ОТКЛОНЕНИЯ

В предыдущем параграфе предполагалось, что точ­ность системы телеуправления определяется значением пролета в конечный момент времени. Такая постановка предполагает, что момент окончания телеуправления tT меньше момента встречи tB. В этом случае этап телеуп­равления не является конечным.

Здесь мы рассмотрим случай, когда tT — tB. При этом ошибка системы телеуправления характеризуется линей­ным отклонением А, под которым понимается длина пер­пендикуляра из точки нахождения объекта наведения на прямую, проходящую через цель под заданным углом.

Предположим, как и ранее, что система телеуправ­ления принадлежит к классу стационарных систем с ко­нечной памятью, а воздействие hz(t) определяется вы­ражением (3.96). Аналогично уравнению (3.99) ошибка системы телеуправления определяется выражением

h(t)=ha(t)-hp(t), (3.117)

где

h p(*)=f *(т)[Аз(*—т)]йГт;

О

n(t)—ошибки измерения, являющиеся белым шу­мом;

k(x)—импульсная переходная функция контура телеуправления.

Динамическая ошибка h^(t) системы может быть оп­ределена с помощью моментных условий (3.102) при — 0

где С2 определяет динамическую ошибку, возникающую при маневре цели, аналогично выражению (ЗДОЗ)

Дисперсия случайной ошибки определяется выраже­нием

г

Dh = N (3.119)

6

где N — уровень спектральной плотности мап(^).

Согласно кинематическим уравнениям ускорение объекта /р связано с линейным Лр уравнением

УР(0.

Дисперсия ускорения /р определяется второй произ­водной от случайной составляющей hp(t), равной hp_c(t). По определению

т

hpc (0= ^k{x)ri{t—x)dx.- (3.121) о

При условии, что

k{Q)=k'{0)=k{T)=k’ {Т)^0, (3.122)

получим

; D,=Nk{T)d-^pdT. (3.123)

о

Далее предлагается решение задачи обеспечения за­данной динамической ошибки при минимуме дисперсии ускорения.

Решение этой задачи позволяет оценить предельные возможности системы наведения по точности при огра­ниченных затратах энергии объекта управления.

Указанная задача сводится к определению импульс­ной переходной функции k (т), минимизирующей (3.123) при условиях (3.118). Используя метод множителей Ла­гранжа, запишем минимизируемый функционал в виде

/=1* k{x)^p-dx — % ^(т)аГт — о о

т т

•“I*! jk(x)xdx — <1>2^т*Л(т)й! т. (3.124)

Оптимальная импульсная функция k(x), минимизи­рующая (3.124), удовлетворяет уравнению

=ф0 + tlT + t2r2, 0 < т < Т. (3. 125)

Решение этого уравнения при граничных условиях (3.122) имеет вид

£л*)=А7′-*)^+’К*+1’2т2% (3-126)

Множители Лагранжа фо, фь Фг определяются под­становкой (3.126) в мом, ентные условия (3.118):

ф =»1_ 36

™ 75 Vі 5 72 )’

ф____ (I______ — ft. V

Ь~ 76 V 5 72 )’

3780/^28 ^ та т З Т2 /

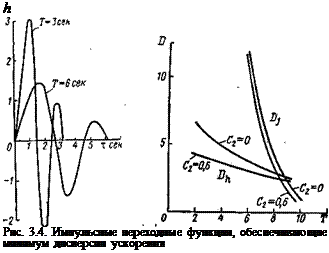
Графики импульсных переходных функций k(x), обеспечивающих минимум дисперсии перегрузки при за­данной динамической точности, приведены на рис. 3.4.

Полученная система обеспечивает дисперсию линей­ного отклонения в виде (3.119).

С „ 21CW

Dh=N J k {X)dx — j437′

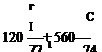
и дисперсию ускорения в виде (3.123) п v Г(ЛЩ%)* . 162007V („

D‘=‘Ni{—j а*=—^г[7-

Графики изменения дисперсии линейного отклонения Dh и ускорения Dj в функции памяти системы Т приве­дены на рис. 3.5 для N— 1 и различных значений CV Известно [17], что оптимальные системы с конечной памятью достаточно сложно реализуются с помощью вы­числительных средств. Для получения простых коррек­тирующих устройств воспользуемся методом, обеспечи­вающим близость характеристик оптимальной k(x) и реализуемой kn (т) систем.

Выберем в качестве приближенной систему, описывае­мую дробно-рациональной передаточной функцией с бес-

конечной памятью. Потребуем, чтобы система обеспечи­вала динамические и случайные ошибки, равные опти­мальным, при условии, что время переходного процесса приближенной системы, определяемое как время измене­ния реакции на единичную ступенчатую функцию, близ­ко к памяти Т оптимальной системы.

Рис. 3.5. Дисперсии линейного
отклонения Dh и ускорения Dj
в функции памяти Т

Импульсную переходную функцию kn(t) запишем в виде [8]

(ЗЛЗО)

* 1-0

Здесь коэффициенты Ai определяются из системы уравнений, обеспечивающей конечность дисперсии уско­рения и заданную динамическую ошибку:

00 1

J К(х) dx = \

О

j* x? k„ (т) dx= — 2 С2.

Время переходного процесса может быть обеспече­но из условия

т

kn(x)dx

о

где е — малая величина.

Дисперсия ускорения в приближенной системе опре­деляется условием

(3.133)

о

где Dj — дисперсия в оптимальной системе (3.129).

Условия (3.132) и (3.133) приводят к нелинейным относительно аг- алгебраическим уравнениям, которые могут быть решены приближенно.

Глава IV